In this article, we will explore how the following topics:
R1CS
Transcript
Selector Polynomial
Vanishing Polynomial
Quadratic Arithmetic Program
R1CS
The term "R1CS" stands for "Rank-1 Constraint System." It's a method used in computer science, particularly in the field of cryptography and zero-knowledge proofs. The Rank-1 Constraint System is a way to express a set of arithmetic constraints. It's commonly used in the construction of zero-knowledge proofs, particularly in systems like zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge).
An R1CS typically consists of three matrices: A, B, and C. Each row in these matrices represents a single constraint, and the system is satisfied if there exists a vector of variables \(\vec{x}\) such that for every row \( \vec{i}\), the following equation holds:
$$\vec{a}_i \cdot \vec{x} \times \vec{b}_i \cdot \vec{x} = \vec{c}_i \cdot \vec{x}$$
Transcript
Trace just means Prover is just going to evaluate this entire circuit and take the values on all the wires. In Interactive proofs, the value of every gate is traced, in Plonk, the trace is defined as the left input, right input, and output of every gate.
QAP: input + output of every multiplication gate.
e.g.:
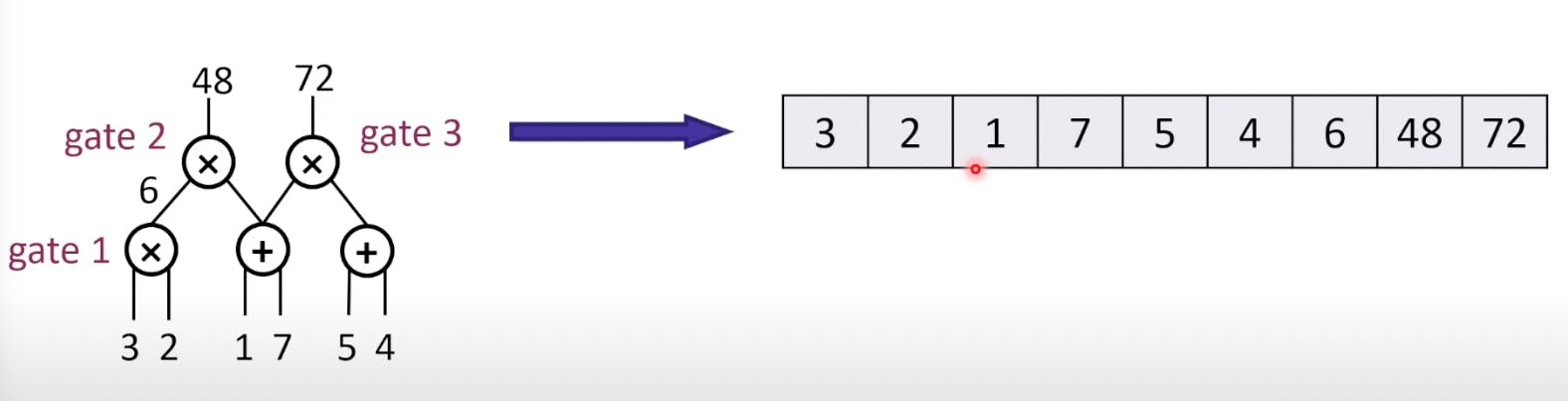
( image credits to Yupeng Zhang )
Selector Polynomial
Let's assume a polynomial \(l_i(x)\) which means is \(c_i\) the left input of gate j, for j = 1,2,3, where \(c_i\) is the value in the i'th position in the transcript ( as in the above image ).
e.g.
\(l_1(x) : (1,0,0)\).
The polynomial interpolation at a known set \(\Omega\) : \(l_1(w) = 1, l_1(w^2) = 0, l_1(w^3) = 0\).\(l_x(x) : (0, 0 ,1)\)
Polynomial interpolation: \(l_3(w) = 0, l_3(w^2) = 0, l_w(w^3) = 0\) since value 1 is the input of the addition gate which in turn is the left input of the multiplication gate ( remember we are taking trace over multiplication gate in case of QAP )
Properties:
\(L(x) = \sum_{i=1}^9 c_i * l_i(x)\). If you write the trace for the entire transcript in the above example: \(L(w) = c_1 = 3\), \(L(w^3) = c_3 + c_4\). The values are the 1s that are present at the respective input column in the entire transpose.
Similarly, we calculate \(r(x)\) and create a transcript then using that a selector polynomial \(R(x)\).
Similarly, we have \(O(x)\) which represents the gate outputs.
Now we have:
$$p(x) = L(x)R(x) - O(x)$$
- Claim is \(p(w^j) = 0 , for \ j = 1,2,3..\)
Vanishing Polynomial
- We define \(p(x) = V(x)q(x)\) , where \(V(x) = (x - w )(x-w^2)(x-w^3)\) is the vanishing polynomial of the set \(\Omega = \{ w, w^2, w^3 \}\)
Finally:
P claims to know a w such that \(C(x,w) = y\) \(<==>\)P claims to know that a vector c such that \(p(x) = V(x)q(x)\).

Where the table is a piece of public information, and generated during preprocessing phase.
Now, instead of checking the constraints in the R1CS individually, we can now check all of the constraints at the same time by doing the dot product check on the polynomials.
Lastly, follow me on social media: Twitter, and LinkedIn for new updates in the cryptography space.
References:

